72 (nùmer)

C'l artìcol chè 'l è scrit in Carpśàn

(S 't î drē a serchèr minga 'l nùmer 72, mo invéci 'l an 72 dòp ch'l era nê Noster Sgnōr, 't ê da 'ndèr chè)

Al 72 (stantadū, settantadue in itagliàṅ, septuaginta duo in latèin) 'l è al nùmer naturèl ( $\mathbb {N}$ ) ch'a seguìs al 71 (stantùn) e 'l vin prìma dal 73 (stantatrī). In dla numerasiòun di romàṅ antìg 'l era scrìt LXXII. In dla numerasiòun ordinèla al tōś al stantaduéśim post.

Proprietê matemàtichi dal 72

'L è 'n nùmer pèra.
Al 72 'l è 'n nùmer cunpòst, send la moltìplica dal 2 col 36:
Fatoriśasiòun: $72=2\cdot 2\cdot 2\cdot 3\cdot 3=2^{3}\cdot 3^{2}$
Al fa pèrt edla séri 'd chi nùmer ch'i ìn la moltìplica 'd 5 nùmer prim, anc cunpàgn tra 'd lōr,^[1]
séri ciamèda anca di nùmer quèśi prim, indû, in cal chèś chè, a s descòr ed nùmer 5-quèśi prim:^[2]
32, 48, 72, 80, 108, 112, 120, 162, 168, 176, 180, 200, 208, 243, 252, 264, 270, 272, 280, 300 ...^[3]
Al 72 al gh'à 12 diviśōr: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.
Send che la sòma di só diviśōr pròpi l'è più granda che lò stès:
1+2+3+4+6+8+9+12+18+24+36 = 123 > 72, dòunca 'l 72 ’l è 'n nùmer abundànt.^[4]^[5]
- 'L è 'n nùmer arfatoriśàbil, send diviśìbil per la quantitê di só diviśōr: $72:12=6$
'L è 'l 15^śim edla sèri di nùmer triangolèr cunsèintric, gnend dòp dal 63 e prìma edl 81:^[6]
1, 3, 6, 9, 12, 15, 19, 24, 30, 36, 42, 48, 55, 63, 72, 81, 90, 99, 109, 120, 132, 144, 156 ...^[7]
'L è 'l 8^èv edla séri di nùmer oblùng, a dìr chi nùmer moltìplica per 2 di nùmer triangolèr:^[8]
2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462 ...^[9]
'L è 'l 4^rt edla sèri di nùmer otadecagonèl cunsèintric, gnend dòp dal 37 e prìma dal 109:^[10]
1, 18, 37, 72, 109, 162, 217, 288, 361, 450, 541, 648, 757, 882, 1009, 1152, 1297, 1458 ...^[11]
'L è 'l 3^rs edla sequèinsa ed chi nùmer ch'i ìn la moltìplica per 12 'd un nùmer triangolèr:^[12]
12, 36, 72, 120, 180, 252, 336, 432, 540, 660, 792, 936, 1092, 1260, 1440, 1632, 1836 ...^[13]
che difàt: $72=12\cdot 6$
'L è 'l 3^rs edla sequèinsa di nùmer 25-gonèl, gnend dòp dal 25 e prìma dal 142:^[14]
1, 25, 72, 142, 235, 351, 490, 652, 837, 1045, 1276, 1530, 1807, 2107, 2430, 2776, 3145 ...^[15]
'L è 'l 2^nd edla sequèinsa di nùmer 72-gonèl, gnend dòp edl 1 e prìma dal 213:
1, 72, 213, 424, 705, 1056, 1477, 1968, 2529, 3160, 3861, 4632, 5473, 6384, 7365, 8416, 9537 ...
'L è 'n nùmer n cun piò solusiòun al'equasiòun φ(x) = n che 'n èter nùmer piò bàs.
Queschè 'l al fà 'n nùmer altamèint totĵnt.
'L è 'n nùmer 'd Ulam.
'L è 'n nùmer 'd Harshad.
'L è 'n nùmer potèint.
Al fà pert edla séri di nùmer idònev:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 15, 16, 18, 21, 22, 24, 25, 28, 30, 33, 37, 40, 42, 45, 48, 57, 58, 60,
70, 72, 78, 85, 88, 93, 102, 105, 112, 120, 130, 133, 165, 168, 177, 190, 210, 232, 240, 253, 273, 280,
312, 330, 345, 357, 385, 408, 462, 520, 760, 840, 1320, 1365 e 1848.^[16]

'L è 'l 8^èv edla sequèinsa di nùmer sòma ed 2 nùmer cub pośitìv, che difàt $72=2^{3}+4^{3}$ $72=2^{3}+4^{3}$ ^[17]
2, 9, 16, 28, 35, 54, 65, 72, 91, 126, 128, 133, 152, 189, 217, 224, 243, 250, 280, 341, 344 ...^[18]
- al 5^nt edla sequèinsa di nùmer sòma ed 2 nùmer cub pośitìv ch'i sìen anc diferèint tra 'd lōr:^[19]
  9, 28, 35, 65, 72, 91, 126, 133, 152, 189, 217, 224, 243, 280, 341, 344, 351, 370, 407, 468 ...^[20]
'L è 'l 6^st edla séri 'd chi nùmer ch'i ìn la sòma ed 4 nùmer prim, ùn drē cl èter: $72=13+17+19+23$
17, 26, 36, 48, 60, 72, 88, 102, 120, 138, 152, 168, 184, 202, 220, 240, 258, 272, 290, 306, 324, 348 ...^[21]^[22]
'L è 'l 3^rs edla séri 'd chi nùmer ch'i ìn la sòma ed 6 nùmer prim ùn drē cl èter: $72=5+7+11+13+17+19$
41, 56, 72, 90, 112, 132, 156, 180, 204, 228, 252, 280, 304, 330, 358, 384, 410, 434, 462, 492, 522, 552 ...^[23]^[24]

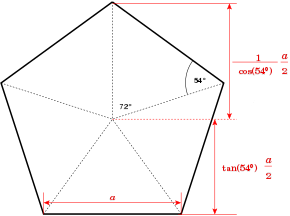
Al nùmer 72 in dla Giometrìa

In dla giometrìa piàna, i àngol ed fóra 'd un pentàgon regolèr egl'ìn ed 72° p'r òun.

Al nùmer 72 in dla Chìmica

Al 72 'l è al nùm'r atómic edl afni (Hf).

I simbol dal nùmer 72

In dla śmòrfia ed Napol

In dla śmòrfia, al nùmer 72 al vōl dìr "la maravìa" ('a maraviglia in napoletàṅ, damànd ch'a gìsen la meraviglia in itagliàṅ).

Vóś lighèdi

Referèinsi

↑ (EN) 'N elèinc dimòndi gros ed chi nùmer ch'i ìn la moltìplica 'd 5 nùmer prim, anc cunpàgn tra 'd lōr, in dal sit edl’OEIS.
↑ (EN) La spiegasiòun di nùmer quèśi prim in dal sit mathworld.wolfram.com.
↑ (EN) Sequèinsa OEIS A014614 'd chi nùmer ch'i ìn la moltìplica 'd 5 nùmer prim, anc cunpàgn tra 'd lōr.
↑ (EN) 'N elèinc dimòndi gros di nùmer abundànt in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A005101 di nùmer abundànt in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer triangolèr cunsèintric in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A194273 di nùmer triangolèr cunsèintric in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer oblùng in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A002378 di nùmer oblùng in dal web.
↑ (EN) 'N elèinc dimòndi gròs di nùmer otadecagonèl cunsèintric in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A195147 di nùmer otadecagonèl cunsèintric in dal web.
↑ (EN) 'N elèinc dimòndi gros ed chi nùmer ch'i ìn la moltìplica per 12 'd un nùmer triangolèr in dal sit edl’OEIS.
↑ (EN) Sequèinsa A049598 ed chi nùmer ch'i ìn la moltìplica per 12 'd un nùmer triangolèr.
↑ (EN) 'N elèinc dimòndi gros di nùmer 25-gonèl in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A255184 di nùmer 25-gonèl in dal web.
↑ (EN) Sequèinsa OEIS A000926 di nùmer idònev in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer sòma ed 2 nùmer cub pośitìv in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A003325 di nùmer sòma ed 2 nùmer cub pośitìv in dal web.
↑ (EN) 'N elèinc dimòndi gros di nùmer sòma ed 2 nùmer cub pośitìv ch'i sìen anc diferèint tra 'd lōr in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A024670 di nùmer sòma ed 2 nùmer cub pośitìv ch'i sìen anc diferèint tra 'd lōr in dla réda.
↑ (EN) 'N elèinc dimòndi gros ed nùmer sòma ed 4 nùmer prim, ùn drē cl èter, in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A034963 di nùmer sòma ed 4 nùmer prim, ùn drē cl èter.
↑ (EN) 'N elèinc dimòndi gros di nùmer sòma ed 6 nùmer prim ùn drē cl èter, in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A127333 di nùmer sòma ed 6 nùmer prim ùn drē cl èter.

Èter progèt

Wikimedia Commons contiene file multimediali su 72 (nùmer)
Wikizionario contiene la voce di dizionario «72 (nùmer)»

Colegamèint estèren

(EN) La sequèinsa OEIS A014614 di nùmer 5-quèśi prim in dla réda.
(EN) La spiegasiòun di nùmer quèśi prim in dal sit mathworld.wolfram.com.
(EN) La sequèinsa OEIS A005101 di nùmer abundànt in dal web.
(EN) La spiegasiòun dal nùmer abundànt in The Prime Glossary.
(EN) Al nùmer abundànt in dal sit mathworld.wolfram.com.
(EN) Al nùmer abundànt spieghê in dal sit planetmath.org.
(EN) La sequèinsa OEIS A194273 di nùmer triangolèr cunsèintric in dla réda.
(EN) La sequèinsa OEIS A002378 di nùmer oblùng in dal web.
(EN) La sequèinsa OEIS A195147 di nùmer otadecagonèl cunsèintric in dla réda.
(EN) La sequèinsa OEIS A255184 di nùmer 25-gonèl in dal web.
(EN) Na spiegasiòun di nùmer figurê dl'Elena Deza e 'd Michel Deza in PDF, 2011.
(EN) La sequèinsa OEIS A000926 di nùmer idònev in dla réda.
(EN) La sèri di nùmer idònev in dal sit MathWorld.
(EN) Al nùmer 72 in tùti el sequèinsi 'd intēr indû 'l s cata, elenchèdi in dal sit edl’OEIS.

[1] (EN) 'N elèinc dimòndi gros ed chi nùmer ch'i ìn la moltìplica 'd 5 nùmer prim, anc cunpàgn tra 'd lōr, in dal sit edl’OEIS.

[2] (EN) La spiegasiòun di nùmer quèśi prim in dal sit mathworld.wolfram.com.

[3] (EN) Sequèinsa OEIS A014614 'd chi nùmer ch'i ìn la moltìplica 'd 5 nùmer prim, anc cunpàgn tra 'd lōr.

[4] (EN) 'N elèinc dimòndi gros di nùmer abundànt in dal sit edl’OEIS.

[5] (EN) Sequèinsa OEIS A005101 di nùmer abundànt in dla réda.

[6] (EN) 'N elèinc dimòndi gros di nùmer triangolèr cunsèintric in dal sit edl’OEIS.

[7] (EN) Sequèinsa OEIS A194273 di nùmer triangolèr cunsèintric in dla réda.

[8] (EN) 'N elèinc dimòndi gros di nùmer oblùng in dal sit edl’OEIS.

[9] (EN) Sequèinsa OEIS A002378 di nùmer oblùng in dal web.

[10] (EN) 'N elèinc dimòndi gròs di nùmer otadecagonèl cunsèintric in dal sit edl’OEIS.

[11] (EN) Sequèinsa OEIS A195147 di nùmer otadecagonèl cunsèintric in dal web.

[12] (EN) 'N elèinc dimòndi gros ed chi nùmer ch'i ìn la moltìplica per 12 'd un nùmer triangolèr in dal sit edl’OEIS.

[13] (EN) Sequèinsa A049598 ed chi nùmer ch'i ìn la moltìplica per 12 'd un nùmer triangolèr.

[14] (EN) 'N elèinc dimòndi gros di nùmer 25-gonèl in dal sit edl’OEIS.

[15] (EN) Sequèinsa OEIS A255184 di nùmer 25-gonèl in dal web.

[16] (EN) Sequèinsa OEIS A000926 di nùmer idònev in dla réda.

[17] (EN) 'N elèinc dimòndi gros di nùmer sòma ed 2 nùmer cub pośitìv in dal sit edl’OEIS.

[18] (EN) Sequèinsa OEIS A003325 di nùmer sòma ed 2 nùmer cub pośitìv in dal web.

[19] (EN) 'N elèinc dimòndi gros di nùmer sòma ed 2 nùmer cub pośitìv ch'i sìen anc diferèint tra 'd lōr in dal sit edl’OEIS.

[20] (EN) Sequèinsa OEIS A024670 di nùmer sòma ed 2 nùmer cub pośitìv ch'i sìen anc diferèint tra 'd lōr in dla réda.

[21] (EN) 'N elèinc dimòndi gros ed nùmer sòma ed 4 nùmer prim, ùn drē cl èter, in dal sit edl’OEIS.

[22] (EN) Sequèinsa OEIS A034963 di nùmer sòma ed 4 nùmer prim, ùn drē cl èter.

[23] (EN) 'N elèinc dimòndi gros di nùmer sòma ed 6 nùmer prim ùn drē cl èter, in dal sit edl’OEIS.

[24] (EN) Sequèinsa OEIS A127333 di nùmer sòma ed 6 nùmer prim ùn drē cl èter.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]