Nùmer poligonèl sentrê

C'l artìcol chè 'l è scrit in Carpśàn

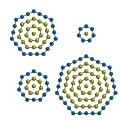
In dla matemàtica giomètrica i nùmer poligonèl sentrê i ìn na clas ed séri ed nùmer naturèl ( $\mathbb {N}$ ) ch'i gh'la chèven anca ed figùrer di polìgon mìs sù con di pùnt (el só unitê), mìs in fila ùn adrē a cl èter, a fèr sù chi polìgon lè ùn dèint'r a c'l èter tùt intór'n a 'l ùnic punt ch'a gh'stà in dal mèś.

Soquànt nùmer etagonèl sentrê figurê.
Soquànt nùmer otagonèl sentrê figurê.
Soquànt nùmer nonagonêl sentrê figurê.
Soquànt nùmer decagonèl sentrê figurê.

Cal sèri chè i ìn quisti chè ch'a seguìs:

nùmer triangolèr sentrê: 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, 571, 631, 694, 760, 829, 901, 976, 1054, 1135, 1219, 1306, 1396, 1489, 1585, 1684, 1786, 1891, 1999, 2110 ...^[1]^[2]
nùmer quadrê sentrê: 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761, 841, 925, 1013, 1105, 1201, 1301, 1405, 1513, 1625, 1741, 1861, 1985, 2113 ...^[3]
nùmer pentagonèl sentrê: 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, 951, 1051, 1156, 1266, 1381, 1501, 1626, 1756, 1891, 2031, 2176 ...^[4]
nùmer eśagonèl sentrê: 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919, 1027, 1141, 1261, 1387, 1519, 1657, 1801, 1951, 2107 ...^[5]
nùmer etagonèl sentrê: 1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, 547, 638, 736, 841, 953, 1072, 1198, 1331, 1471, 1618, 1772, 1933, 2101, 2276 ...^[6]^[7]
nùmer otagonèl sentrê: 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089, 1225, 1369, 1521, 1681, 1849, 2025, 2209, 2401 ...^[8]
nùmer enagonèl sentrê: 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946, 1081, 1225, 1378, 1540, 1711, 1891, 2080, 2278, 2485, 2701 ...^[9]^[10]
nùmer decagonèl sentrê: 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, 781, 911, 1051, 1201, 1361, 1531, 1711, 1901, 2101, 2311, 2531, 2761 ...
nùmer endecagonèl sentrê: 1, 12, 34, 67, 111, 166, 232, 309, 397, 496, 606, 727, 859, 1002, 1156, 1321, 1497, 1684, 1882, 2091, 2311, 2542, 2784 ...^[11]^[12]
nùmer dodecagonèl sentrê: 1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793, 937, 1093, 1261, 1441, 1633, 1837, 2053, 2281, 2521, 2773 ...^[13]^[14]
nùmer tridecagonèl sentrê: 1, 14, 40, 79, 131, 196, 274, 365, 469, 586, 716, 859, 1015, 1184, 1366, 1561, 1769, 1990, 2224, 2471, 2731, 3004 ...^[15]^[16]
nùmer tetradecagonèl sentrê: 1, 15, 43, 85, 141, 211, 295, 393, 505, 631, 771, 925, 1093, 1275, 1471, 1681, 1905, 2143, 2395, 2661, 2941, 3235 ...^[17]^[18]
nùmer pentadecagonèl sentrê: 1, 16, 46, 91, 151, 226, 316, 421, 541, 676, 826, 991, 1171, 1366, 1576, 1801, 2041, 2296, 2566, 2851, 3151, 3466 ...^[19]^[20]
nùmer eśadecagonèl sentrê: 1, 17, 49, 97, 161, 241, 337, 449, 577, 721, 881, 1057, 1249, 1457, 1681, 1921, 2177, 2449, 2737, 3041, 3361, 3697 ...^[21]^[22]
nùmer etadecagonèl sentrê: 1, 18, 52, 103, 171, 256, 358, 477, 613, 766, 936, 1123, 1327, 1548, 1786, 2041, 2313, 2602, 2908, 3231, 3571, 3928 ...^[23]^[24]
nùmer otadecagonèl sentrê: 1, 19, 55, 109, 181, 271, 379, 505, 649, 811, 991, 1189, 1405, 1639, 1891, 2161, 2449, 2755, 3079, 3421, 3781, 4159 ...^[25]^[26]
nùmer enadecagonèl sentrê: 1, 20, 58, 115, 191, 286, 400, 533, 685, 856, 1046, 1255, 1483, 1730, 1996, 2281, 2585, 2908, 3250, 3611, 3991, 4390 ...^[27]^[28]
nùmer 20-gonèl sentrê: 1, 21, 61, 121, 201, 301, 421, 561, 721, 901, 1101, 1321, 1561, 1821, 2101, 2401, 2721, 3061, 3421, 3801, 4201, 4621 ...^[29]^[30]
nùmer 21-gonèl sentrê: 1, 22, 64, 127, 211, 316, 442, 589, 757, 946, 1156, 1387, 1639, 1912, 2206, 2521, 2857, 3214, 3592, 3991, 4411, 4852 ...^[31]^[32]
nùmer 22-gonèl sentrê: 1, 23, 67, 133, 221, 331, 463, 617, 793, 991, 1211, 1453, 1717, 2003, 2311, 2641, 2993, 3367, 3763, 4181, 4621, 5083 ...^[33]^[34]
nùmer 23-gonèl sentrê: 1, 24, 70, 139, 231, 346, 484, 645, 829, 1036, 1266, 1519, 1795, 2094, 2416, 2761, 3129, 3520, 3934, 4371, 4831, 5314 ...^[35]^[36]
nùmer 24-gonèl sentrê: 1, 25, 73, 145, 241, 361, 505, 673, 865, 1081, 1321, 1585, 1873, 2185, 2521, 2881, 3265, 3673, 4105, 4561, 5041, 5545 ...^[37]^[38]
nùmer 25-gonèl sentrê: 1, 26, 76, 151, 251, 376, 526, 701, 901, 1126, 1376, 1651, 1951, 2276, 2626, 3001, 3401, 3826, 4276, 4751, 5251, 5776 ...^[39]
nùmer 26-gonèl sentrê: 1, 27, 79, 157, 261, 391, 547, 729, 937, 1171, 1431, 1717, 2029, 2367, 2731, 3121, 3537, 3979, 4447, 4941, 5461, 6007 ...
nùmer 27-gonèl sentrê: 1, 28, 82, 163, 271, 406, 568, 757, 973, 1216, 1486, 1783, 2107, 2458, 2836, 3241, 3673, 4132, 4618, 5131, 5671, 6238 ...
nùmer 28-gonèl sentrê: 1, 29, 85, 169, 281, 421, 589, 785, 1009, 1261, 1541, 1849, 2185, 2549, 2941, 3361, 3809, 4285, 4789, 5321, 5881, 6469 ...^[40]^[41]
nùmer 29-gonèl sentrê: 1, 30, 88, 175, 291, 436, 610, 813, 1045, 1306, 1596, 1915, 2263, 2640, 3046, 3481, 3945, 4438, 4960, 5511, 6091, 6700 ...
nùmer 30-gonèl sentrê: 1, 31, 91, 181, 301, 451, 631, 841, 1081, 1351, 1651, 1981, 2341, 2731, 3151, 3601, 4081, 4591, 5131, 5701, 6301, 6931 ...
nùmer 31-gonèl sentrê: 1, 32, 94, 187, 311, 466, 652, 869, 1117, 1396, 1706, 2047, 2419, 2822, 3256, 3721, 4217, 4744, 5302, 5891, 6511, 7162 ...
nùmer 32-gonèl sentrê: 1, 33, 97, 193, 321, 481, 673, 897, 1153, 1441, 1761, 2113, 2497, 2913, 3361, 3841, 4353, 4897, 5473, 6081, 6721, 7393 ...^[42]^[43]
nùmer 33-gonèl sentrê: 1, 34, 100, 199, 331, 496, 694, 925, 1189, 1486, 1816, 2179, 2575, 3004, 3466, 3961, 4489, 5050, 5644, 6271, 6931, 7624 ...
nùmer 34-gonèl sentrê: 1, 35, 103, 205, 341, 511, 715, 953, 1225, 1531, 1871, 2245, 2653, 3095, 3571, 4081, 4625, 5203, 5815, 6461, 7141, 7855 ...
nùmer 35-gonèl sentrê: 1, 36, 106, 211, 351, 526, 736, 981, 1261, 1576, 1926, 2311, 2731, 3186, 3676, 4201, 4761, 5356, 5986, 6651, 7351, 8086 ...
nùmer 36-gonèl sentrê: 1, 37, 109, 217, 361, 541, 757, 1009, 1297, 1621, 1981, 2377, 2809, 3277, 3781, 4321, 4897, 5509, 6157, 6841, 7561, 8317 ...^[44]^[45]
nùmer 37-gonèl sentrê: 1, 38, 112, 223, 371, 556, 778, 1037, 1333, 1666, 2036, 2443, 2887, 3368, 3886, 4441, 5033, 5662, 6328, 7031, 7771, 8548 ...
nùmer 38-gonèl sentrê: 1, 39, 115, 229, 381, 571, 799, 1065, 1369, 1711, 2091, 2509, 2965, 3459, 3991, 4561, 5169, 5815, 6499, 7221, 7981, 8779 ...
nùmer 39-gonèl sentrê: 1, 40, 118, 235, 391, 586, 820, 1093, 1405, 1756, 2146, 2575, 3043, 3550, 4096, 4681, 5305, 5968, 6670, 7411, 8191, 9010 ...
nùmer 40-gonèl sentrê: 1, 41, 121, 241, 401, 601, 841, 1121, 1441, 1801, 2201, 2641, 3121, 3641, 4201, 4801, 5441, 6121, 6841, 7601, 8401, 9241 ...^[46]^[47]
nùmer 41-gonèl sentrê: 1, 42, 124, 247, 411, 616, 862, 1149, 1477, 1846, 2256, 2707, 3199, 3732, 4306, 4921, 5577, 6274, 7012, 7791, 8611, 9472 ...
nùmer 42-gonèl sentrê: 1, 43, 127, 253, 421, 631, 883, 1177, 1513, 1891, 2311, 2773, 3277, 3823, 4411, 5041, 5713, 6427, 7183, 7981, 8821, 9703 ...
nùmer 43-gonèl sentrê: 1, 44, 130, 259, 431, 646, 904, 1205, 1549, 1936, 2366, 2839, 3355, 3914, 4516, 5161, 5849, 6580, 7354, 8171, 9031, 9934 ...
nùmer 44-gonèl sentrê: 1, 45, 133, 265, 441, 661, 925, 1233, 1585, 1981, 2421, 2905, 3433, 4005, 4621, 5281, 5985, 6733, 7525, 8361, 9241, 10165 ...^[48]^[49]
nùmer 45-gonèl sentrê: 1, 46, 136, 271, 451, 676, 946, 1261, 1621, 2026, 2476, 2971, 3511, 4096, 4726, 5401, 6121, 6886, 7696, 8551, 9451, 10396 ...
nùmer 46-gonèl sentrê: 1, 47, 139, 277, 461, 691, 967, 1289, 1657, 2071, 2531, 3037, 3589, 4187, 4831, 5521, 6257, 7039, 7867, 8741, 9661, 10627 ...
nùmer 47-gonèl sentrê: 1, 48, 142, 283, 471, 706, 988, 1317, 1693, 2116, 2586, 3103, 3667, 4278, 4936, 5641, 6393, 7192, 8038, 8931, 9871, 10858 ...^[50]
nùmer 48-gonèl sentrê: 1, 49, 145, 289, 481, 721, 1009, 1345, 1729, 2161, 2641, 3169, 3745, 4369, 5041, 5761, 6529, 7345, 8209, 9121, 10081, 11089 ...
nùmer 49-gonèl sentrê: 1, 50, 148, 295, 491, 736, 1030, 1373, 1765, 2206, 2696, 3235, 3823, 4460, 5146, 5881, 6665, 7498, 8380, 9311, 10291, 11320 ...
nùmer 50-gonèl sentrê: 1, 51, 151, 301, 501, 751, 1051, 1401, 1801, 2251, 2751, 3301, 3901, 4551, 5251, 6001, 6801, 7651, 8551, 9501, 10501, 11551 ...
nùmer 51-gonèl sentrê: 1, 52, 154, 307, 511, 766, 1072, 1429, 1837, 2296, 2806, 3367, 3979, 4642, 5356, 6121, 6937, 7804, 8722, 9691, 10711, 11782 ...

...

... e via acsè ...

Proprietê

Per tùt i intēr k ≥ 3, al prìm nùmer k-gonèl sentrê 'l è 'l 1.
'L n-éśum poligonèl sentrê, ch'a s cata śuntènd (n – 1)k a quèl ch'al vin prìma, 'l è dòunca 1 + k volti la sòma di intēr da 'l 1 a 'l n – 1, o anca 1 + k volti 'l (n – 1)-éśim nùmer triangolèr^[51]:

C_{k,n}=1+k+2k+\ldots (n-1)k=1+k{\frac {n(n-1)}{2}}=1+kT_{n-1}

Vóś lighèdi

Noti e referèinsi

↑ (EN) 'N elèinc dimòndi gros di nùmer triangolèr sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A005448 di nùmer triangolèr sentrê.
↑ (EN) Sequèinsa OEIS A001844 di nùmer quadrê sentrê.
↑ (EN) Sequèinsa OEIS A005891 di nùmer pentagonèl sentrê in dla réda.
↑ (EN) Sequèinsa OEIS A003215 di nùmer eśagonèl sentrê in dal web.
↑ (EN) 'N elèinc dimòndi gros di nùmer etagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069099 di nùmer etagonèl sentrê in dla réda.
↑ (EN) Sequèinsa OEIS A016754 di nùmer otagonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer enagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A060544 di nùmer enagonèl sentrê in dal web.
↑ (EN) 'N elèinc dimòndi gròs di nùmer endecagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069125 di nùmer endecagonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gròs di nùmer dodecagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A003154 di nùmer dodecagonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer tridecagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069126 di nùmer tridecagonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer tetradecagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069127 di nùmer tetradecagonèl sentrê in dal web.
↑ (EN) 'N elèinc dimòndi gròs di nùmer pentadecagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069128 di nùmer pentadecagonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer eśadecagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069129 di nùmer eśadecagonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer etadecagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069130 di nùmer etadecagonèl sentrê, in dal web.
↑ (EN) 'N elèinc dimòndi gros di nùmer otadecagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069131 di nùmer otadecagonèl sentrê.
↑ (EN) 'N elèinc dimòndi gros di nùmer enadecagonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069132 di nùmer enadecagonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gròs di nùmer 20-gonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069133 di nùmer 20-gonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gròs di nùmer 21-gonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069178 di nùmer 21-gonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer 22-gonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069173 di nùmer 22-gonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer 23-gonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069174 di nùmer 23-gonèl sentrê in dal web.
↑ (EN) 'N elèinc dimòndi gròs di nùmer 24-gonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A069190 di nùmer 24-gonèl sentrê in dla réda.
↑ (EN) Sequèinsa OEIS A262221 di nùmer 25-gonèl sentrê in dal web.
↑ (EN) 'N elèinc dimòndi gros di nùmer 28-gonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A195314 di nùmer 28-gonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer 32-gonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A195315 di nùmer 32-gonèl sentrê in dal web.
↑ (EN) 'N elèinc dimòndi gros di nùmer 36-gonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A195316 di nùmer 36-gonèl sentrê in dla réda.
↑ (EN) 'N elèinc dimòndi gros di nùmer 40-gonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A195317 di nùmer 40-gonèl sentrê in dal web.
↑ (EN) 'N elèinc dimòndi gros di nùmer 44-gonèl sentrê in dal sit edl’OEIS.
↑ (EN) Sequèinsa OEIS A195318 di nùmer 44-gonèl sentrê in dla réda.
↑ (EN) Sequèinsa OEIS A129428 di nùmer 47-gonèl sentrê in dal web.
↑ (EN) La spiegasiòun in dal lìber Figurate numbers 'd Elena Deza, Michel Marie Deza, ed. World Scientific, 2012, in sìm'a Google books.

Èter progèt

Wikimedia Commons contiene file multimediali su Nùmer poligonèl sentrê

Colegamèint estèren

(EN) Al nùmer poligonèl sentrê in dal sit mathworld.com.
(EN) Na spiegasiòun di nùmer figurê dl'Elena Deza e 'd Michel Deza in PDF, 2011.

[1] (EN) 'N elèinc dimòndi gros di nùmer triangolèr sentrê in dal sit edl’OEIS.

[2] (EN) Sequèinsa OEIS A005448 di nùmer triangolèr sentrê.

[3] (EN) Sequèinsa OEIS A001844 di nùmer quadrê sentrê.

[4] (EN) Sequèinsa OEIS A005891 di nùmer pentagonèl sentrê in dla réda.

[5] (EN) Sequèinsa OEIS A003215 di nùmer eśagonèl sentrê in dal web.

[6] (EN) 'N elèinc dimòndi gros di nùmer etagonèl sentrê in dal sit edl’OEIS.

[7] (EN) Sequèinsa OEIS A069099 di nùmer etagonèl sentrê in dla réda.

[8] (EN) Sequèinsa OEIS A016754 di nùmer otagonèl sentrê in dla réda.

[9] (EN) 'N elèinc dimòndi gros di nùmer enagonèl sentrê in dal sit edl’OEIS.

[10] (EN) Sequèinsa OEIS A060544 di nùmer enagonèl sentrê in dal web.

[11] (EN) 'N elèinc dimòndi gròs di nùmer endecagonèl sentrê in dal sit edl’OEIS.

[12] (EN) Sequèinsa OEIS A069125 di nùmer endecagonèl sentrê in dla réda.

[13] (EN) 'N elèinc dimòndi gròs di nùmer dodecagonèl sentrê in dal sit edl’OEIS.

[14] (EN) Sequèinsa OEIS A003154 di nùmer dodecagonèl sentrê in dla réda.

[15] (EN) 'N elèinc dimòndi gros di nùmer tridecagonèl sentrê in dal sit edl’OEIS.

[16] (EN) Sequèinsa OEIS A069126 di nùmer tridecagonèl sentrê in dla réda.

[17] (EN) 'N elèinc dimòndi gros di nùmer tetradecagonèl sentrê in dal sit edl’OEIS.

[18] (EN) Sequèinsa OEIS A069127 di nùmer tetradecagonèl sentrê in dal web.

[19] (EN) 'N elèinc dimòndi gròs di nùmer pentadecagonèl sentrê in dal sit edl’OEIS.

[20] (EN) Sequèinsa OEIS A069128 di nùmer pentadecagonèl sentrê in dla réda.

[21] (EN) 'N elèinc dimòndi gros di nùmer eśadecagonèl sentrê in dal sit edl’OEIS.

[22] (EN) Sequèinsa OEIS A069129 di nùmer eśadecagonèl sentrê in dla réda.

[23] (EN) 'N elèinc dimòndi gros di nùmer etadecagonèl sentrê in dal sit edl’OEIS.

[24] (EN) Sequèinsa OEIS A069130 di nùmer etadecagonèl sentrê, in dal web.

[25] (EN) 'N elèinc dimòndi gros di nùmer otadecagonèl sentrê in dal sit edl’OEIS.

[26] (EN) Sequèinsa OEIS A069131 di nùmer otadecagonèl sentrê.

[27] (EN) 'N elèinc dimòndi gros di nùmer enadecagonèl sentrê in dal sit edl’OEIS.

[28] (EN) Sequèinsa OEIS A069132 di nùmer enadecagonèl sentrê in dla réda.

[29] (EN) 'N elèinc dimòndi gròs di nùmer 20-gonèl sentrê in dal sit edl’OEIS.

[30] (EN) Sequèinsa OEIS A069133 di nùmer 20-gonèl sentrê in dla réda.

[31] (EN) 'N elèinc dimòndi gròs di nùmer 21-gonèl sentrê in dal sit edl’OEIS.

[32] (EN) Sequèinsa OEIS A069178 di nùmer 21-gonèl sentrê in dla réda.

[33] (EN) 'N elèinc dimòndi gros di nùmer 22-gonèl sentrê in dal sit edl’OEIS.

[34] (EN) Sequèinsa OEIS A069173 di nùmer 22-gonèl sentrê in dla réda.

[35] (EN) 'N elèinc dimòndi gros di nùmer 23-gonèl sentrê in dal sit edl’OEIS.

[36] (EN) Sequèinsa OEIS A069174 di nùmer 23-gonèl sentrê in dal web.

[37] (EN) 'N elèinc dimòndi gròs di nùmer 24-gonèl sentrê in dal sit edl’OEIS.

[38] (EN) Sequèinsa OEIS A069190 di nùmer 24-gonèl sentrê in dla réda.

[39] (EN) Sequèinsa OEIS A262221 di nùmer 25-gonèl sentrê in dal web.

[40] (EN) 'N elèinc dimòndi gros di nùmer 28-gonèl sentrê in dal sit edl’OEIS.

[41] (EN) Sequèinsa OEIS A195314 di nùmer 28-gonèl sentrê in dla réda.

[42] (EN) 'N elèinc dimòndi gros di nùmer 32-gonèl sentrê in dal sit edl’OEIS.

[43] (EN) Sequèinsa OEIS A195315 di nùmer 32-gonèl sentrê in dal web.

[44] (EN) 'N elèinc dimòndi gros di nùmer 36-gonèl sentrê in dal sit edl’OEIS.

[45] (EN) Sequèinsa OEIS A195316 di nùmer 36-gonèl sentrê in dla réda.

[46] (EN) 'N elèinc dimòndi gros di nùmer 40-gonèl sentrê in dal sit edl’OEIS.

[47] (EN) Sequèinsa OEIS A195317 di nùmer 40-gonèl sentrê in dal web.

[48] (EN) 'N elèinc dimòndi gros di nùmer 44-gonèl sentrê in dal sit edl’OEIS.

[49] (EN) Sequèinsa OEIS A195318 di nùmer 44-gonèl sentrê in dla réda.

[50] (EN) Sequèinsa OEIS A129428 di nùmer 47-gonèl sentrê in dal web.

[51] (EN) La spiegasiòun in dal lìber Figurate numbers 'd Elena Deza, Michel Marie Deza, ed. World Scientific, 2012, in sìm'a Google books.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

v · d · m Nùmer figurê
Nùmer poligonèl	Nùmer triangolèr • Nùmer quadrê • Nùmer pentagonèl • Nùmer eśagonèl • Nùmer etagonèl • Nùmer otagonèl • Nùmer enagonèl • Nùmer decagonèl • Nùmer endecagonèl • Nùmer dodecagonèl • Nùmer tridecagonèl • Nùmer tetradecagonèl • Nùmer pentadecagonèl • Nùmer eśadecagonèl • Nùmer etadecagonèl • Nùmer otadecagonèl • Nùmer enadecagonèl • Nùmer icośagonèl • Nùmer 21-gonèl • Nùmer 22-gonèl • Nùmer 23-gonèl • Nùmer 24-gonèl • Nùmer 25-gonèl • Nùmer 26-gonèl • Nùmer 27-gonèl • Nùmer 28-gonèl • Nùmer 29-gonèl • Nùmer 30-gonèl • Nùmer 31-gonèl • Nùmer 32-gonèl • Nùmer 33-gonèl • Nùmer 34-gonèl • Nùmer 35-gonèl • Nùmer 36-gonèl • Nùmer 37-gonèl • Nùmer 38-gonèl • Nùmer 39-gonèl • Nùmer 40-gonèl • Nùmer 41-gonèl • Nùmer 42-gonèl • Nùmer 43-gonèl • Nùmer 44-gonèl • Nùmer 45-gonèl • Nùmer 46-gonèl • Nùmer 47-gonèl • Nùmer 48-gonèl • Nùmer 49-gonèl • Nùmer 50-gonèl • Nùmer 51-gonèl • Nùmer oblùng
Nùmer poligonèl sentrê	Nùmer triangolèr sentrê • Nùmer quadrê sentrê • Nùmer pentagonèl sentrê • Nùmer eśagonèl sentrê • Nùmer etagonèl sentrê • Nùmer otagonèl sentrê • Nùmer enagonèl sentrê • Nùmer decagonèl sentrê • Nùmer endecagonèl sentrê • Nùmer dodecagonèl sentrê • Nùmer tridecagonèl sentrê • Nùmer tetradecagonèl sentrê • Nùmer pentadecagonèl sentrê • Nùmer eśadecagonèl sentrê • Nùmer etadecagonèl sentrê • Nùmer otadecagonèl sentrê • Nùmer enadecagonèl sentrê • Nùmer 20-gonèl sentrê • Nùmer 21-gonèl sentrê • Nùmer 22-gonèl sentrê • Nùmer 23-gonèl sentrê • Nùmer 24-gonèl sentrê • Nùmer 25-gonèl sentrê • Nùmer 26-gonèl sentrê • Nùmer 27-gonèl sentrê • Nùmer 28-gonèl sentrê • Nùmer 29-gonèl sentrê • Nùmer 30-gonèl sentrê • Nùmer 31-gonèl sentrê • Nùmer 32-gonèl sentrê • Nùmer 33-gonèl sentrê • Nùmer 34-gonèl sentrê • Nùmer 35-gonèl sentrê • Nùmer 36-gonèl sentrê • Nùmer 37-gonèl sentrê • Nùmer 38-gonèl sentrê • Nùmer 39-gonèl sentrê • Nùmer 40-gonèl sentrê • Nùmer 41-gonèl sentrê • Nùmer 42-gonèl sentrê • Nùmer 43-gonèl sentrê • Nùmer 44-gonèl sentrê • Nùmer 45-gonèl sentrê • Nùmer 46-gonèl sentrê • Nùmer 47-gonèl sentrê • Nùmer 48-gonèl sentrê • Nùmer 49-gonèl sentrê • Nùmer 50-gonèl sentrê • Nùmer 51-gonèl sentrê • Nùmer stelê
Nùmer poliédric	Nùmer tetraédric • Nùmer piramidèl quadrê • Nùmer piramidèl pentagonèl • Nùmer piramidèl eśagonèl • Nùmer piramidèl etagonèl • Nùmer piramidèl otagonèl • Nùmer piramidèl enagonèl • Nùmer piramidèl decagonèl • Nùmer piramidèl endecagonèl • Nùmer piramidèl dodecagonèl • Nùmer piramidèl tridecagonèl • Nùmer piramidèl tetradecagonèl • Nùmer piramidèl pentadecagonèl • Nùmer piramidèl eśadecagonèl • Nùmer piramidèl etadecagonèl • Nùmer piramidèl otadecagonèl • Nùmer piramidèl enadecagonèl • Nùmer piramidèl 20-gonèl • Nùmer piramidèl 21-gonèl • Nùmer piramidèl 22-gonèl • Nùmer piramidèl 23-gonèl • Nùmer piramidèl 24-gonèl • Nùmer piramidèl 25-gonèl • Nùmer piramidèl 26-gonèl • Nùmer piramidèl 27-gonèl • Nùmer piramidèl 28-gonèl • Nùmer piramidèl 29-gonèl • Nùmer piramidèl 30-gonèl • Nùmer piramidèl 31-gonèl • Nùmer piramidèl 32-gonèl • Nùmer piramidèl 33-gonèl • Nùmer piramidèl 34-gonèl • Nùmer piramidèl 35-gonèl • Nùmer piramidèl 36-gonèl • Nùmer piramidèl 37-gonèl • Nùmer piramidèl 38-gonèl • Nùmer piramidèl 39-gonèl • Nùmer piramidèl 40-gonèl • Nùmer piramidèl 41-gonèl • Nùmer piramidèl 42-gonèl • Nùmer piramidèl 43-gonèl • Nùmer piramidèl 44-gonèl • Nùmer piramidèl 45-gonèl • Nùmer piramidèl 46-gonèl • Nùmer piramidèl 47-gonèl • Nùmer piramidèl 48-gonèl • Nùmer piramidèl 49-gonèl • Nùmer piramidèl 50-gonèl • Nùmer piramidèl 51-gonèl • Nùmer otaédric • Nùmer otaédric tronchê • Nùmer stèla otangolèr • Nùmer cubic • Nùmer cùbic sentrê
Nùmer politòpic	Nùmer pentatòpic • Nùmer ipercùbic
Dl èter	Tioréma 'd Fermat in sim'ai nùmer poligonèl